News
In 2018, researchers from the Harvard John A. Paulson School of Engineering and Applied Sciences (SEAS) made a surprising discovery. For decades, physicists had been trying to understand the dynamics of crumpled materials — how thin, flat sheets develop disordered, three-dimensional networks of folds and creases. The question was, does crumpling follow some kind of general rule or rules?
The answer could help physicists understand how everything from graphene sheets to tectonic plates crumple and could help engineers design better materials for a range of applications from quantum computing to solar sails.
Through a series of experiments, the researchers found that there was, in fact, order in the chaos. The team repeatedly crumpled and uncrumpled thin sheets of Mylar, which form creases similarly to conventional paper. They observed that while each individual sheet developed a unique crease pattern, the total crease length on each sheet grew logarithmically.
Simulation of the crumpling of a Mylar sheet, which form creases similarly to conventional paper. (Video courtesy of Jovana Andrejević/Harvard SEAS)
“It’s surprising that this seemingly chaotic system follows any rule at all, but it’s really surprising that it follows a simple logarithm,” said Christopher Rycroft, the John L. Loeb Associate Professor of Engineering and Applied Sciences at SEAS, and one of the co-authors of the 2018 study.
But why?
That question is the focus of a new paper by Rycroft and his team, published in Nature Communications.
“From the previous research, we knew that the logarithmic growth of crease length was a robust phenomenon that could be reproduced over and over again but we were missing the physical basis for why this happens,” said Jovana Andrejevic, a graduate student at SEAS and first author of the paper.
To answer that question, the researchers looked at the flat sections of Mylar between the creases.
“We wanted to know how these individual regions between the creases evolved over time,” said Rycroft.
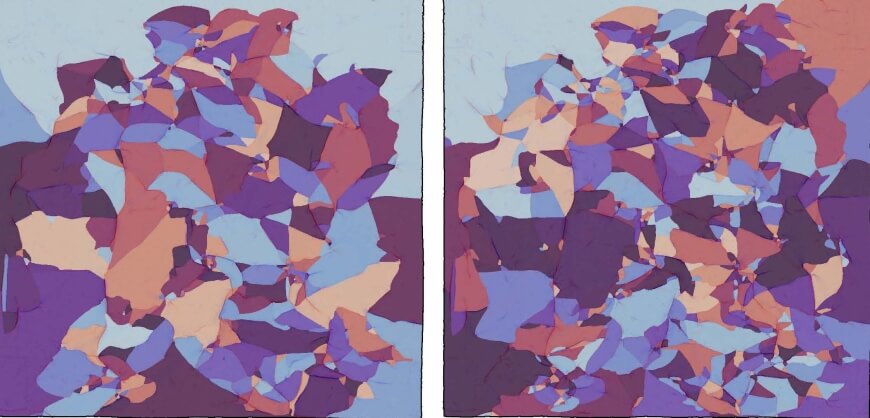
But the network of creases on the crumpled Mylar was incredibly chaotic and automated algorithms had a hard time sifting through the noise to find those regions. So, Andrejevic, who is also an artist, decided to trace the creases by hand. The painstaking and meticulous process took hours, sometimes days, to complete for each sheet. But, in the end, it revealed a new way to understand the process of crumpling.
Hand-traced creases reveal how larger regions break up into several smaller regions. (Image courtesy of Jovana Andrejevic/Harvard SEAS)
Download ImageDownload Image
“If you look at how these regions evolve as the paper is crumpled again and again, you see that the larger regions break up into several smaller regions, just like how a pebble on the beach will break up into smaller pieces over time,” said Rycroft.
Physicists have already developed a theory, known as fragmentation theory, to describe the process of how larger objects break up into smaller objects.
When the team applied the mathematical framework of fragmentation theory to the crumpled sheets, they found that the framework matched the data almost perfectly and could predict the logarithmic scaling result.
“It highlights the idea that there are universal principles uniting seemingly diverse, disordered systems, such as crumpled paper and fragmented rocks,” said Andrejevic.
“Crumpling is a window into how materials are damaged through disordered processes, like networks of cracks forming, and how they fail,” said Rycroft. “The model gives us a framework for thinking about how other materials fail, and how we might design and fabricate materials to avoid this.”
The paper was co-authored by Lisa Lee and Shmuel M. Rubinstein. This research was partially supported by the National Science Foundation through the Harvard University Materials Research Science and Engineering Center under grant no. DMR-2011754. The research was also supported by the National Science Foundation under grant DGE-1745303, and the U.S. DOE Office of Science Advanced Scientific Computing Research under Contract No. DE-AC02-05CH11231
Topics: Applied Physics
Cutting-edge science delivered direct to your inbox.
Join the Harvard SEAS mailing list.
Scientist Profiles
Christopher Rycroft
Associate in Materials Science and Mechanical Engineering
Press Contact
Leah Burrows | 617-496-1351 | lburrows@seas.harvard.edu